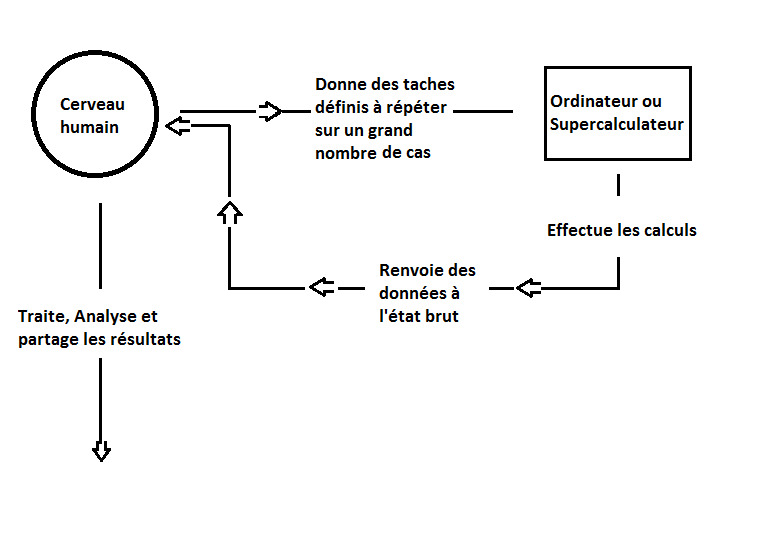
Complémentarité entre le cerveau et l'ordinateur dans le domaine des mathématiques appliquées
Maintenant que nous avons vu les caractéristiques propres à l'ordinateur et au cerveau, il nous faut voir comment ces différences, mais aussi ces ressemblances font de ces deux « machines » (l'une biologique et l'autre mécanique) des outils complémentaires pour la recherche et la résolution de problèmes dans différents secteurs des sciences, mais aussi de la vie courante. Il est important de préciser que pour la plupart de ces exemples, l'utilisation de la machine permet de faire des découvertes qui n'auraient pu être réalisables à l'échelle humaine, au vu de la longueur des recherches ou de la complexité des calculs.
Mathématiques appliquées

Les premières recherches de théorème (énoncé dont l'exactitude peut être mathématiquement démontrée) en mathématiques sont datées de 2 millénaires avant Jésus-Christ, c'est-à-dire au tout début de l'âge de bronze. Pourtant 4000 ans plus tard, des mathématiciens continuent ce genre de recherches puisqu'ils existent actuellement près de 800 célèbre théoremes. Alors que Thalès ou Pythagore ont du trouver, chercher et démontrer leur théorème seul et avec comme seule aide leur cerveau, il n'est plus du tout rare de nos jours de voir des mathématiciens utiliser la puissance de calculs des ordinateurs, qui leurs permet éviter de longs et fastidieux calculs ou encore tout simplement de réussir à finir de démontrer leurs théorèmes dans l'espace d'une vie humaine. Cet élément peut nous paraitre ridicule, quand l'on entends parler de personnes comme Pythagore ou Newton qui démontrèrent nombreux théorèmes durant leurs vies. Pourtant réussir à fonder un théorème reconnus par les mathématiciens et autres scientifiques n'est pas aussi sipmle. Prenons par exemple le théorème de Fermat, qui durant près de 400 ans resta irrésolus malgrés les nombreuses recherches d'iminent scientifiques de leurs époques.
Le premier théorème résolu entièrement à l'aide d'une machine est le théorème des quatre couleurs. Ce théorème fut conjecturé en 1852 par Francis Guthrie et résolu en 1976 par Kenneth Appel et Wolfgang Hakenc c'est à dire qu'il a fallu un siècle pour résoudre cette enigme.
Le théorème ennonce la vérité suivante :
"Il est possible, en n'utilisant que quatre couleurs différentes,de colorer n'importe quelle découpée en régions connexes, de sorte que deux régions adjacentes ou limitrophes,c'est-à-dire ayant toute une frontière (et non simplement un point) en commun reçoivent toujours deux couleurs distinctes "

De nombreux mathématiciens tentèrent de le résoudre, mais même les plus célèbre chercheurs ne réussirent qu'à donner de fausses démonstrations ou des théorèmes moins important, comme celui des 5 couleurs. C'est en 1879 que Kempe introduit une notion qui sera fondamentale pour résoudre cette conjecture :
Il voulut démontrer que toute carte normale contenait une face avec cinq voisines au plus et qu'une face ayant deux, trois, quatre ou cinq voisines était « réductible », c'est-à-dire qu'il existe une autre façon de disposer les couleurs en en utilisant une de moins. En répétant ce procédé, on obtient ainsi des configurations irréductibles et si une configuration irréductible nécessite plus de 4 couleurs, le théorème est faux. Malheureusement Kempe se trompa lui aussi et ne réussit pas à résoudre cette énigme mathématique. Mais c'est grâce à l'apport de personnes n'ayant pas réussi que le théorème avancait. En effet Kempe par exemple, avec sa notion de configurations réductible et irréductible, posa les fondements des outils utilisé pour la démonstration final.
Appel et Haken découvrirent que les configurations réductibles étaient réduisible à un ensemble d'environ 2000 cartes et que chacune de ces cartes pouvaient être représentée sous la forme d'un graphe planaire.
Et c'est ainsi qu'à l'aide d'un algorithme programmé par eux même et d'ordinateurs type IBM 370-168 qu'ils commencèrent à réduire à sa forme irréductible chaque carte ou graphes de l'ensemble. L'ordinateur prenait 6 minutes pour les cas simples et plus de 15 minutes pour les cas compliqués. Ils démontrèrent ainsi que la conjecture formulée par Guthrie s'avérait vraie !
Nous pouvons maintenant constater que ce théorème n'aurait absolument pas pu être résolu de façons simple sans l'aide d'une machine. Il suffit pour cela de regarder le temps pris par chaque "intervenant", l'IBM d’Appel et Haken prenait une moyenne de 11 minutes par cas, et il y avait 2000 cas. Cela revient à 370 heures de calculs pour une machine, certes peu puissante. Maintenant, imaginons qu'un humain prennent 10 fois le temps mis par la machine pour chaque cas, cela reviens à passer 7 mois jours et nuits sans jamais s'arrêter ni se tromper. Cela dépasse les capacités humaines actuelles. De plus ce travail très répétitif ne serait prisé par personne pour le résultat qu'il offrirait.
Appel et Haken expliquèrent ceci à propos de leurs programmes :
« Le programme commença à donner des résultats surprenants. Au début, nous vérifiions à la main ces arguments, de façon à prévoir son comportement dans toutes les situations possibles ; puis tout à coup, il commença à se comporter comme une machine à jouer aux échecs. Il combinait des stratégies fondées sur tous les trucs qu'on lui avait appris, et souvent ces méthodes s'avéraient plus efficaces que celles que nous aurions spontanément utilisées. Il commença ainsi à nous faire découvrir des procédés inattendus. En un certain sens, il avait dépassé ces créateurs pour les tâches intellectuelles et pour les tâches mécaniques. »
Nous pouvons sentir un certaine enthousiasme de la part de ces deux chercheurs, cepedant il faut regarder la résolution de ce problème dans la globalité pour comprendre ou et comment l'ordinateur et le cerveau se sont passé le relai.En premier lieu, c'est un cerveau humain qui en 1852 conjectura le problème, mais c'est aussi un cerveau humain qui introduit la logique des ensembles réductible et irréductible qui fut utilisée pour ce problème et enfin ce sont deux cerveaux humains qui développèrent l'algorithme néscéssaire à l'ordinateur. Finallement, c'est l'ordinateur qui résolus inlassablement ce problème. Grâce à la compléxité de l'algorythme, l'ordinateur a pu prendre des déscision sur la résolution de certains cas, comme le montre la citation précédente.
Dans ce problème, l'être humain a fourni des paramètres précis et définis à l'ordinateur, qui à l'aide d'une logique primaire et répétitive, créer par Appel et Haken, a pu réduire les 2000 cartes ou graphes de l'ensemble et ainsi démontrer le théorème des quatres couleurs.
Conclusion
L'ordinateur n'aurait pu créer, définir, généraliser et numériser ce problème et réciproquement l'être humain n'aurait pu résoudre (et pourtant de nombreux ont essayé) par manque de temps, de moyens, de rapidité de calcul. Il est clair que dans cet exemple, ordinateur et cerveau ont travaillé "main dans la main" si l'on peux dire, pour résoudre un problème d'une envergure remarquable.